Ir al contenido principal

Mecánica: Movimiento Rectilíneo Acelerado

Movimiento Rectilíneo Acelerado

Índice

  1. Movimiento Rectilíneo Acelerado
  2. Caída Libre Unidimensional
  3. Respuestas

Movimiento Rectilíneo Acelerado

  1. Un vehículo lleva una velocidad de $72\ \mbf{km/h}$ y se encuentra con un muro a $50\ \mbf{m}$. Si frena con una aceleración constante de $2{,}0\ \mbf{m/s^2}$ ¿Logra detenerse antes de chocar?
  2. Un tren se desplaza por una vía recta. En cierto instante de tiempo se mueve con velocidad de $36\ \mbf{km/h}$. Un observador que va en la cabina de mando comprueba que cada $20\ \mbf s$ el tren aumenta su velocidad en $18\ \mbf{km/h}$.
    1. Calcule la aceleración del tren.
    2. Escriba la ecuación de la velocidad.
    3. Calcule la velocidad del tren tras $110\ \mbf s$.
  3. Un automóvil está parado en un semáforo. Cuando se enciende la luz verde arranca con aceleración constante de $2{,}0\ \mbf{ m/s^2}$. En el momento de arranca el auto, un camión con velocidad constante de $54\ \mbf{km/h}$ lo adelanta.
    1. ¿Cuánto tiempo transcurre hasta que el auto adelanta al camión?
    2. ¿A qué distancia del semáforo lo alcanza?
    3. ¿Qué velocidad lleva el auto en ese momento?
  4. En un cruce existe una señalética que indica que el límite de velocidad es $40\ \mbf{km/h}$. Una camioneta pasa por el cruce a una velocidad de $72\ \mbf{km/h}$, que mantiene constante. En ese momento arranca desde el cruce una moto de la policía en la misma dirección y sentido, alcanzando una velocidad de $108\ \mbf{km/h}$ en $10\ \mbf s$. El motorista mantienene constante esta velocidad.
    1. ¿Cuánto tarda la moto en alcanzar a la camioneta?
    2. Respecto del cruce ¿A qué distancia alcanza el policía a la camioneta?
    3. Si a los $100\ \mbf m$ desde que ocurre el alcance se detienen ambos vehículos ¿Cuál ha sido la aceleración de cada uno?
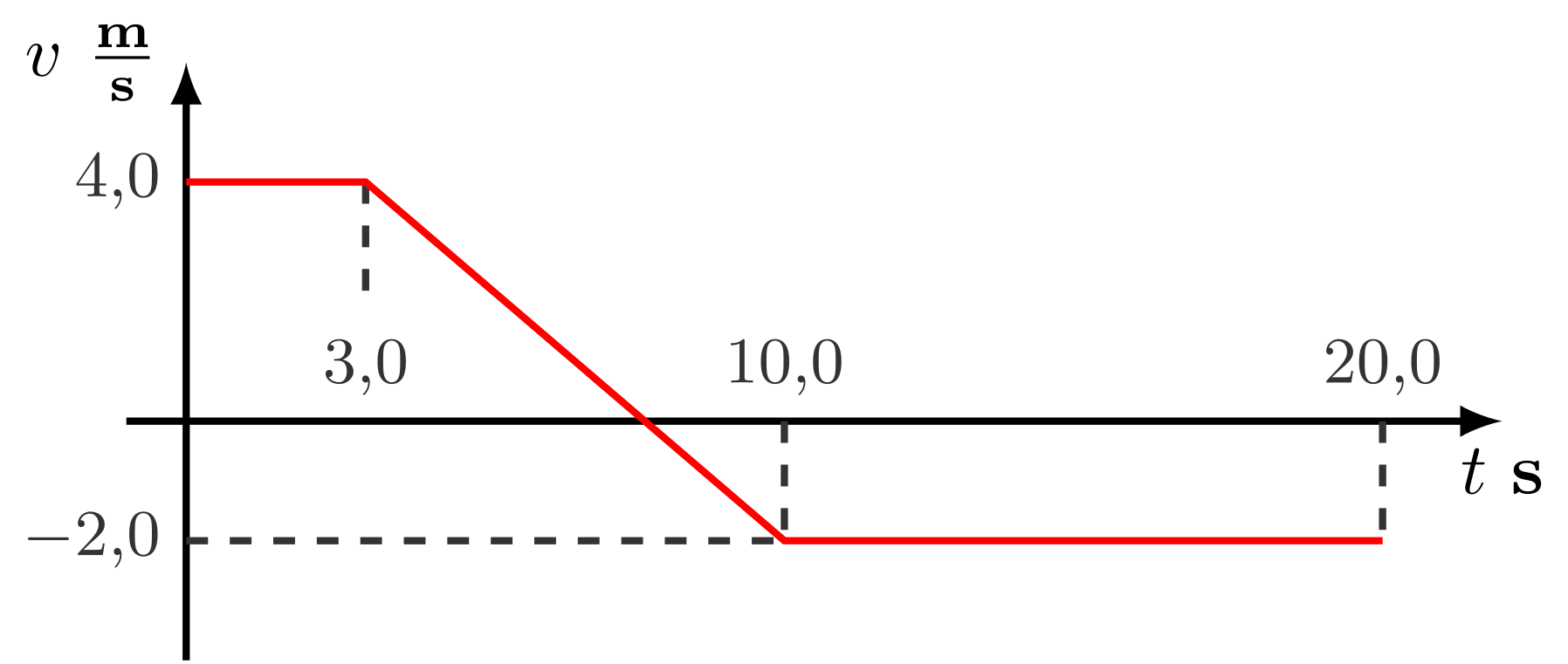
  5. Considere el siguiente gráfico de la velocidad en función del tiempo de una partícula que se mueve a lo largo del eje $y$ Vector A
    1. Determine $v(t)$.
    2. Encuentre $a(t)$.
    3. Si en $t=0{,}0\ \mbf{s}$ la posición es $y=5{,}0\ \mbf{m}$, obtenga la posición como función del tiempo.
    4. Esboce el gráfico posición versus tiempo.

    Indicación: Utilice funciones definidas por tramo.

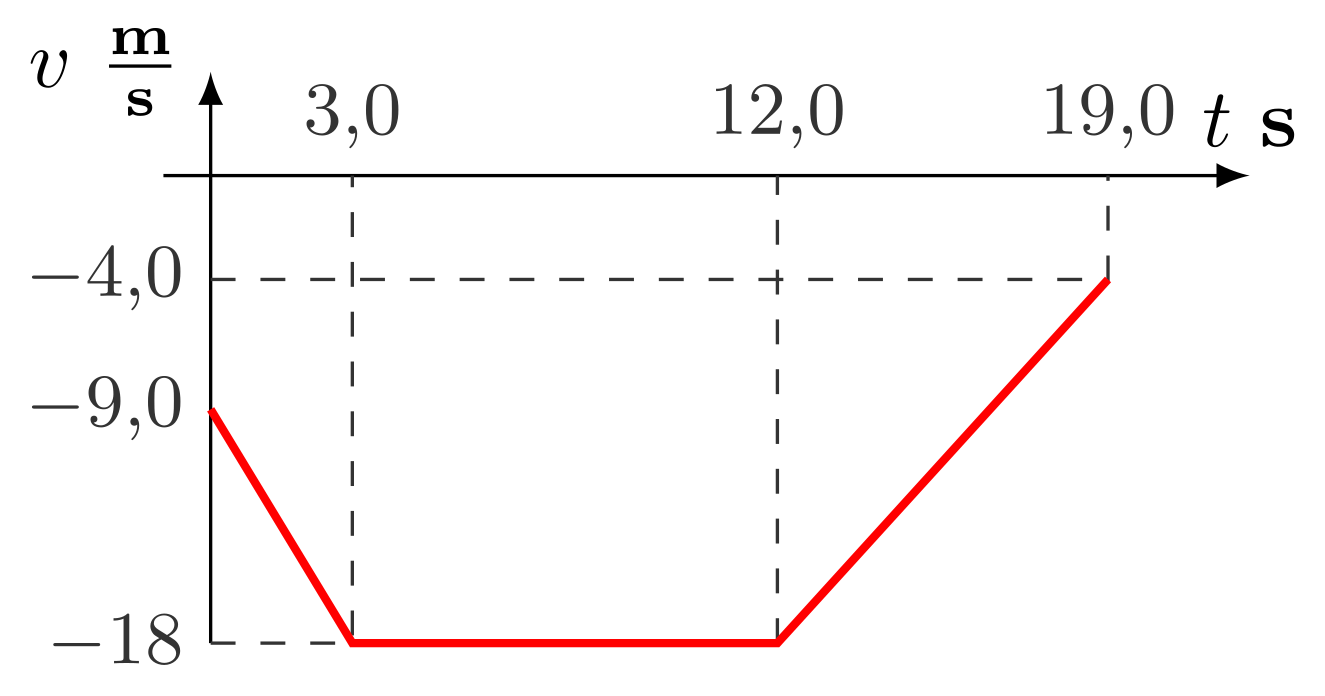
  6. Considere el siguiente gráfico de la aceleración en función del tiempo de una partícula que se mueve a lo largo del eje $z$ Vector A
    1. Considere que la velocidad en $t=5{,}0\ \mbf{s}$ es $v=-18\ \mbf{m/s}$. Encuentre la velocidad como función del tiempo y esboce la respectiva gráfica.
    2. Si en $t=10\ \mbf{s}$ la posición es $z=0{,}0\ \mbf{m}$, obtenga la posición como función del tiempo.
    3. Esboce el gráfico posición versus tiempo.

    Indicación: Utilice funciones definidas por tramo.

Caída Libre Unidimensional

  1. Se lanza una pelota verticalmente hacia arriba con una velocidad de $20\ \mbf{m/s}$. Calcule el tiempo que tarda en volver al suelo.
  2. Un globo se está elevando a $2{,}0\ \mbf{m/s}$ . Cuando el globo se encuentra a $50\ \mbf m$ de altitud se deja caer una piedra. Determine
    1. La velocidad inicial de la piedra.
    2. El tiempo que tarda en llegar al suelo.
    3. La velocidad con que llega la piedra al suelo.
  3. Se lanza verticalmente hacia arriba desde el suelo, un cuerpo con velocidad inicial de $15\ \mbf{m/s}$. Despreciando la acción del aire, obtenga
    1. La altura máxima alcanzada.
    2. El tiempo que tarda en subir.
  4. Desde una altura de $80\ \mbf m$ se deja caer una piedra. Dos segundos después se lanza otra desde el suelo en la misma vertical con una velocidad de $50\ \mbf{m/s}$. Determine
    1. El instante de tiempo en que se encuentran las piedras.
    2. La altura a la que se produce el encuentro.
  5. Se dispara verticalmente hacia arriba un proyectil con una velocidad de $200\ \mbf{m/s}$, al cabo de $4{,}00\ \mbf s$, se lanza un segundo proyectil con la misma velocidad. Calcule
    1. La altura a la que se encuentran.
    2. El tiempo que tardan en encontrarse.
    3. La velocidad de cada proyectil en el momento en que se encuentran.

Respuestas

Movimiento Rectilíneo Acelerado

  1. No. Se detendría $50\ \mbf m$ más allá del muro.
  2. Si el tren avanza en la dirección positiva del eje $x$
    1. $\vec a=0{,}25\,\hat\imath\ \mbf{m/s^2}$.
    2. $\vec v(t)=(10+0{,}25\,t)\,\hat\imath\ \mbf{m/s}$
    3. $\vec v(t=110\ \mbf{s})=38\,\hat\imath\, \mbf{m/s}$
    1. Transcurren $15\ \mbf s$.
    2. A $2{,}2\times 10^2\ \mbf m$ ($225\ \mbf m$) del semáforo.
    3. $v=30\ \mbf {m/s}$ hacia adelante.
    1. Tarda $15\ \mbf s$.
    2. $3{,}0\times 10^2\ \mbf{m}$ ($300\ \mbf m$) más adelante del cruce.
    3. $a_c=-2{,}0\ \mbf{m/s^2}$ y $a_m=-4{,}5\ \mbf{m/s^2}$.
    1. $$v(t)=\left\{\begin{array}{l} 4{,}0\ \mbf{m/s}&\text{si, } 0{,}0\leq t\leq 3{,}0\ \mbf s\\ \Bigl(4{,}0-0{,}86(t-3{,}0)\Bigr)\ \mbf{m/s}&,\ \text{si } 3{,}0< t\leq 10{,}0\ \mbf s\\ -2{,}0\ \mbf{m/s}&\text{si, } 10{,}0< t\leq 20{,}0\ \mbf s \end{array}\right.$$
    2. $$a(t)=\left\{\begin{array}{l} 0{,}0\ \mbf{\frac{m}{s^2}}& ,\ \text{si } 0{,}0\leq t\leq 3{,}0\ \mbf s\\ -0{,}86\ \mbf{\frac{m}{s^2}}& ,\ \text{si } 3{,}0< t\leq 10{,}0\ \mbf s\\ 0{,}0\ \mbf{\frac{m}{s^2}}& ,\ \text{si } 10{,}0< t\leq 20{,}0\ \mbf s \end{array}\right.$$
    3. $$y(t)=\left\{\begin{array}{l} \Bigl(5{,}0+4{,}0\,t\Bigr)\ \mbf{m}&,\ \text{si } 0{,}0\leq t\leq 3{,}0\ \mbf s\\ \Bigl(17+4{,}0(t-3{,}0)-0{,}43(t-3{,}0)^2\Bigr)\ \mbf{m}&,\ \text{si } 3{,}0< t\leq 10{,}0\ \mbf s\\ \Bigl(24-2{,}0(t-10{,}0)\Bigr)\ \mbf{m}&,\ \text{si } 10{,}0< t\leq 20{,}0\ \mbf s \end{array}\right.$$
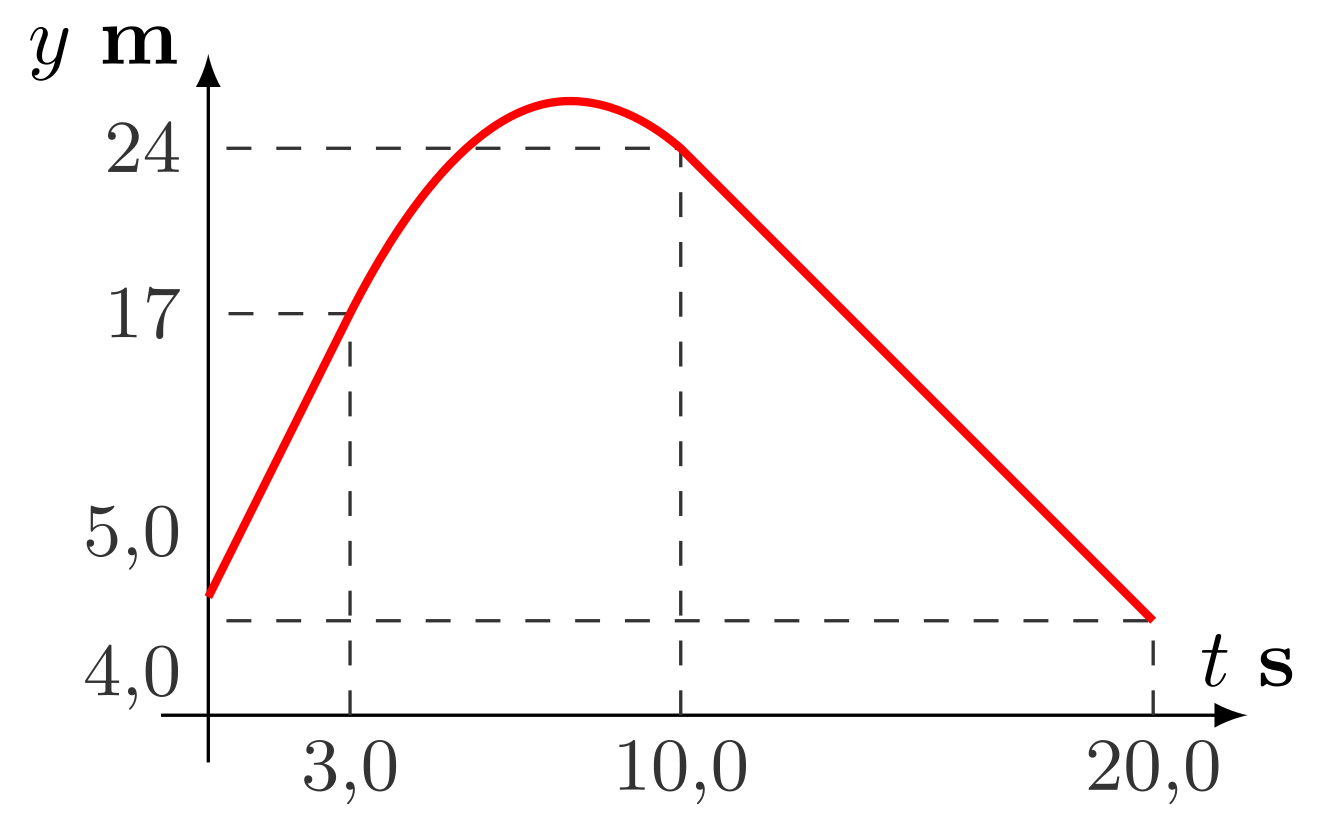
    4. Vector A
    1. $$v(t)=\left\{\begin{array}{l} \Bigl(-18-3{,}0(t-3{,}0)\Bigr)\ \mbf{m/s}&,\ \text{si } 0{,}0\leq t\leq 3{,}0\ \mbf s\\ -18\ \mbf{m/s}&,\ \text{si } 3{,}0< t\leq 12{,}0\ \mbf s\\ \Bigl(-18+2{,}0(t-12{,}0)\Bigr)\ \mbf{m/s}&,\ \text{si } 12{,}0< t\leq 19{,}0\ \mbf s \end{array}\right.$$ Vector A
    2. $$z(t)=\left\{\begin{array}{l} \Bigl(126-18(t-3{,}0)-1{,}5(t-3{,}0)^2\Bigr)\ \mbf{m}&,\ \text{si } 0{,}0\leq t\leq 3{,}0\ \mbf s\\ -18(t-10{,}0)\ \mbf{m}&,\ \text{si } 3{,}0< t\leq 12{,}0\ \mbf s\\ \Bigl(-36-18(t-12{,}0)+(t-12{,}0)^2\Bigr)\ \mbf{m}&,\ \text{si } 12{,}0< t\leq 19{,}0\ \mbf s \end{array}\right.$$ Vector A

Caída Libre Unidimensional

  1. $t=4{,}1\ \mbf s$
  2. Con un eje vertical hacia arriba
    1. $\vec v_0=2{,}0\,\hat\jmath\ \mbf{m/s}$.
    2. $t=3{,}4\ \mbf s$.
    3. $\vec v_\text{suelo}=-31\,\hat\jmath\ \mbf{m/s}$.
    1. $h_\text{max}=11\ \mbf{m}$.
    2. $t=1{,}5\ \mbf s$.
    1. $t=2{,}9\ \mbf s$.
    2. $h_\text{encuentro}=40\ \mbf{m}$.
  5. Con un eje vertical hacia arriba
    1. $h_\text{encuentro}=2{,}02\ \mbf{km}$.
    2. $t=22{,}4\ \mbf s$.
    3. $\vec v_1=-19{,}5\,\hat\jmath\ \mbf{m/s}$ y $\vec v_2=19{,}7\,\hat\jmath\ \mbf{m/s}$

Comentarios

Publicar un comentario

Entradas populares

Mecánica: Movimiento Parabólico y Movimiento Circunferencial

Índice Movimiento Parabólico Movimiento Circunferencial Respuestas Movimiento Parabólico Un proyectil se lanza con una velocidad de $200\ \mbf{m/s}$ formando un ángulo de $30{,}0^\circ$ con la horizontal. Calcule a los $8{,}0\ \mbf s$ de su lanzamiento: El vector velocidad y el ángulo que forma ésta con el eje vertical . El desplazamiento total. En un duelo del lejano Oeste un pistolero dispara horizontalmente una bala con velocidad de $200\ \mbf{m/s}$ desde una altura de $1{,}25\ \mbf{m}$. Calcule la distancia mínima entre los adversarios, para que la presunta víctima no sea alcanzada. Indicación: La bala realiza movimiento parabólico, de modo que en algún momento choca con el suelo y así el adversario no es alcanzado. Desde una altura de $10\ \mbf m$ sobre el suelo, se lanza horizontalmente un objeto con velocidad de $20\ \mbf{m/s}$. Determinar: La distancia horizontal a la que toc
Publicar un comentario
Leer más

Mecánica: Leyes de Newton

Índice Fuerza, masa y aceleración Aplicaciones de las leyes de Newton Respuestas Fuerza, masa y aceleración Sobre una masa de $7{,}00\,\mbf{kg}$ se aplican las siguientes fuerzas: una fuerza de $10{,}0\,\mbf N$ hacia el Norte, una fuerza de $20{,}0\,\mbf N$ al Este y una fuerza de $30{,}0\,\mbf N$ en dirección $30^\circ$ al Sur del Oeste. Obtenga la aceleración de esta masa. La aceleración de gravedad en la superficie del Sol, en la superficie de la Luna y en la superficie de Marte es, $27{,}9\, g$, $0{,}160\, g$ y $0{,}380\, g$, respectivamente, donde $g$ es la aceleración de gravedad en la superficie de la Tierra ($g=9{,}8\,\mbf{m/s^2}$). Calcule el peso de una persona cuya masa es $60{,}0\,\mbf{kg}$ en la superficie del Sol, la Luna, Marte y la Tierra. En la superficie de Mercurio la aceleración de gravedad es $4{,}00\,\mbf{m/s^2}$. Si una sonda espacial pesa $500\,\mbf N$ en la superficie de Mercurio, encuentre el pes
Publicar un comentario
Leer más

Termodinámica: Gases y cambio de fase

Gases y cambio de fase Índice Gases Gases ideales Titulación Constantes, datos y factores de conversión Respuestas Propiedades del agua saturada Tabla de temperaturas SI Tabla de presiones SI Tabla de temperaturas USCS Tabla de presiones USCS Gases Considere un tanque de volumen $V=50{,}0\ \mt{l}$ que contiene $16{,}9\ \mt{kg}$ de argón cuando la temperatura es de $15{,}0^\circ\mt C$. Determine la cantidad de sustancia de argón contenida en el tanque y su volumen molar. Calcule la presión del argón como si fuese un gas ideal. Obtenga la presión utilizando las siguientes ecuaciones de estado. En cada caso ¿Cuál es el valor del factor de compresibilidad? Van der Waals $$\left(p+\frac{a}{{\bar v}^2}\right)(\bar v-b)=RT$$ $a_{_{\ce{Ar}}}=1{,}630\times10^{-2}\ \mt{\frac{Pa\,m^6}{mol^2}}$ $b_{_{\ce{Ar}}}=3{,}201\times10^{-5}\ \mt{\frac{m^3}{mol}}$ Redlich - Kwong $$\left(p+\
Publicar un comentario
Leer más